Adaptive disretization using voronoi tree for continuous pomdps
Many decision making under uncertainty problems can naturally be specified as POMDP problems with continuous state, action and observation spaces. While many effective online POMDP solvers for discrete action and observation spaces exist, solving fully continuous POMDPs remains challenging, particularly for problems with high-dimensional action spaces. To alleviate this difficulty, we propose Adaptive Discretization using Voronoi Trees (ADVT), a new Monte Carlo Tree Search (MCTS) based online POMDP solver. ADVT adaptively partitions the action space for each sampled belief using a hierarchical data structure, called Voronoi Tree -- a Binary Space Partitioning that implicitly maintains the partition of a cell as as the Voronoi Diagram of two points sampled from the cell. This enables ADVT to exploit local structure of the action value function, thereby leading to a more effective exploration of the action space, particularly for higher-dimensional action spaces, compared to existing state-of-the-art methods. Additionally, ADVT handles continuous observation spaces by adopting a progressive widening strategy in combination with a weighted particle representation of beliefs. Empirical results indicate that ADVT scales substantially better to high-dimensional action spaces compare to existing methods. Our C++ implementation of ADVT is available at https://github.com/hoergems/ADVT.
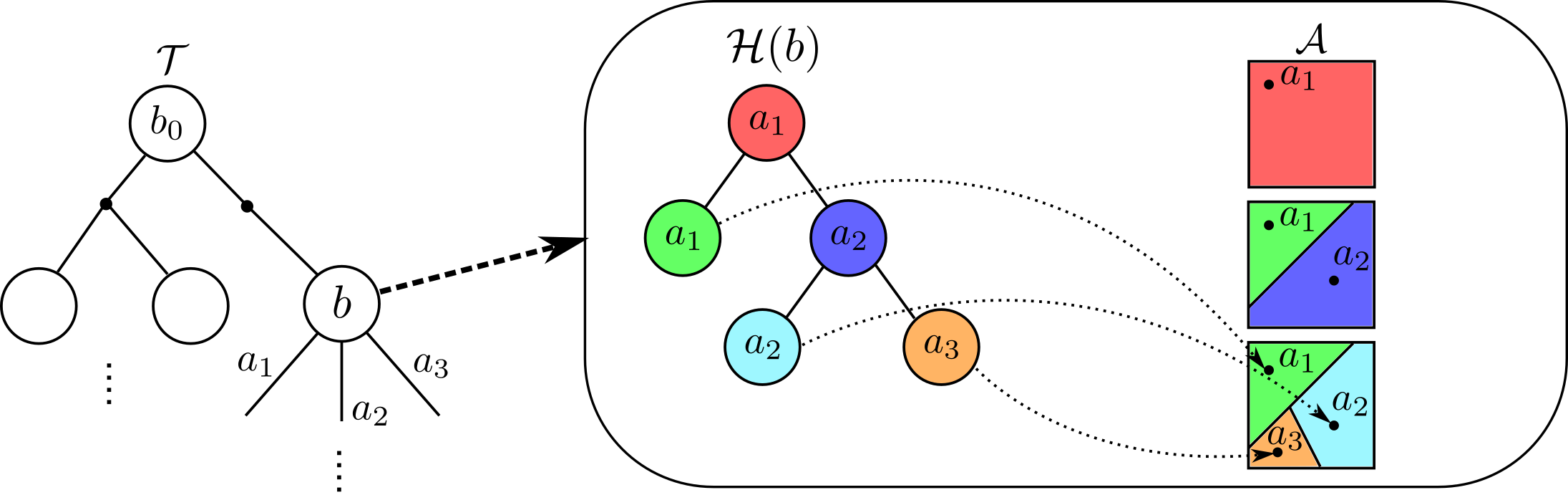
Voronoi Trees
Key to ADVT is the combination of Monte Carlo Tree Search with a new hierarchical partitioning of the action space, called Voronoi Tree, illustrated in Figure 1. A Voronoi Tree is a Binary Space Partitioning (BSP) of the action space, where each partitioning hyperplane is implicitly maintained based on the Voronoi diagram of a pair of sampled representative actions. At each sampled belief, ADVT maintains a Voronoi Tree that is refined adaptively during planning: Cells are refined if they either represent large, unexplored regions of the action space, or contain actions with large estimated values. This enables ADVT to quickly focus its search on the most promising regions of the action space.
Empirical Results
We evaluated ADVT on a set of benchmark POMDP problems with continuous state, action and observation spaces, including a manipulation problem with a 12-dimensional continuous action space. Our results indicate that ADVT scales to higher-dimensional action spaces much more effectively compared to two state-of-the-art online POMDP solvers.

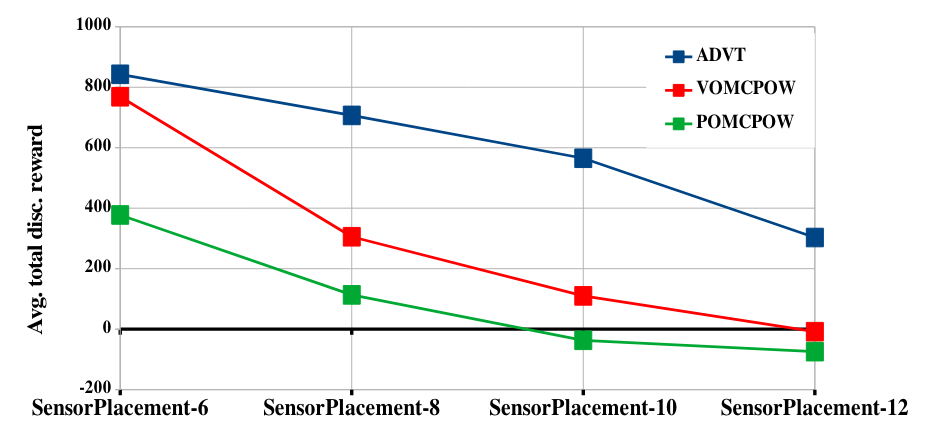
Additional details and results are available in our paper.
References
2024
2023
People
- Marcus Hoerger
- Hanna Kurniawati
- Nan Ye
- Dirk Kroese