Primitives for inspection planning with implicit models

Jingyang You, Hanna Kurniawati and Lashika Medagoda

The aging and increasing complexity of infrastructures makes efficient inspection planning more critical in ensuring safety. Thanks to sampling-based motion planning, many inspection planners are fast. However, they often require huge memory. This is particularly true when the structure under inspection is large and complex, consisting of many struts and pillars of various geometry and sizes. Such structures can be represented efficiently using implicit models, such as neural Signed Distance Functions (SDFs). However, most primitive computations used in sampling-based inspection planner have been designed to work efficiently with explicit environment models, which in turn requires the planner to use explicit environment models or performs frequent transformations between implicit and explicit environment models during planning. This paper proposes a set of primitive computations, called Inspection Planning Primitives with Implicit Models (IPIM), that enable sampling-based inspection planners to entirely use neural SDFs representation during planning. Evaluation on three scenarios, including inspection of a complex real-world structure with over 92M triangular mesh faces, indicates that even a rudimentary sampling-based planner with IPIM can generate inspection trajectories of similar quality to those generated by the state-of-the-art planner, while using up to $70\times$ less memory than the state-of-the-art inspection planner.

The high memory requirements with inspection planning can be reduced using implicit representation of the environments and observation. IPIM proposes efficient primitives when implicit neural-network based SDF representation is used to represent the environment and observation. Neural SDF is recognized for its rapid training and compactness, making it well-suited for planning tasks that demand memory efficiency.
With IPIM, the known explicit environment model $\mathcal{E}$ is first converted into an implicit SDF model $f_{\mathcal{E}}$ represented by a neural network. Without the loss of generality, we suppose IPIM is used with a sampling-based inspection planner that builds a tree $\mathbb{T} = \{ \mathbb{N}, \mathbb{E}\}$, where $\mathbb{N}$ and $\mathbb{E}$ are the set of nodes and edges in the tree. Under IPIM, each node $\mathbf{n} \in \mathbb{N}$ represents a 4-tuple $\left\langle \mathbf{q}, \mathbf{B_{P_n}}, f_\mathbf{P_n}, \textbf{cov($\mathbf{n}$)}\right\rangle$. The four elements in the tuple reflect how IPIM converts the four primitives of the planner to their implicit forms, namely:

Collision Check: $\mathbf{q} \in C_{free}$ refers to a sampled robot's configuration at node $\mathbf{n}$. Denote its parent node as $\mathbf{n}' \in \mathbb{N}$. The collision check against trajectory $\overline{\mathbf{n}'\mathbf{n}}$ is done with the implicit model $f_{\mathcal{E}}$.
Observation Simulation: The observation $\mathbf{P_n}$ (e.g., a depth image), is simulated using the SDF function $f_{\mathcal{E}}$. \textit{For brevity, in the following sections, when we say the bounding box of $\mathbf{P_n}$, we mean the bounding box of the point cloud corresponding to the observation} $\mathbf{P_n}$.
IPIM maintains the bounding box of $\mathbf{P_n}$, denoted as $\mathbf{B_{P_n}}$.
Observation Representation: The local SDF $f_\mathbf{P_n}$ encodes $\mathbf{P_n}$ with a tiny-sized multi-layer perceptron. The set of local surface points, denoted as $S_\mathbf{P_n}$, can then be generated from $\mathbf{B_{P_n}}$ and $f_\mathbf{P_n}$ with marching cube.
Total Coverage Check: cov($\mathbf{n}$) refers to the accumulated coverage in the path from the root of $\mathbb{T}$ until the node $\mathbf{n}$ of $\mathbb{T}$. This coverage is calculated incrementally and implicitly as $\mathbb{T}$ being expanded.

We apply IPIM on a simple RITA-like [1] inspection planner, and benchmark its performace against the state-of-the-art inspection planner IRIS [2] across three scenarios with increasing complexity. We show that IPIM achieves superior memory efficiency in complex and cluttered real-world scenarios. The scenarios are briefly introduced below.

Experiment scenarios. From left to right: Bridge, Plant-s and Plant

Bridge with 7.4K mesh vertices and 9.4K mesh faces, taken from [2]. We have reduced the scale of this environment by a factor of ten, so it has size 6m $\times$ 2m $\times$ 4m.
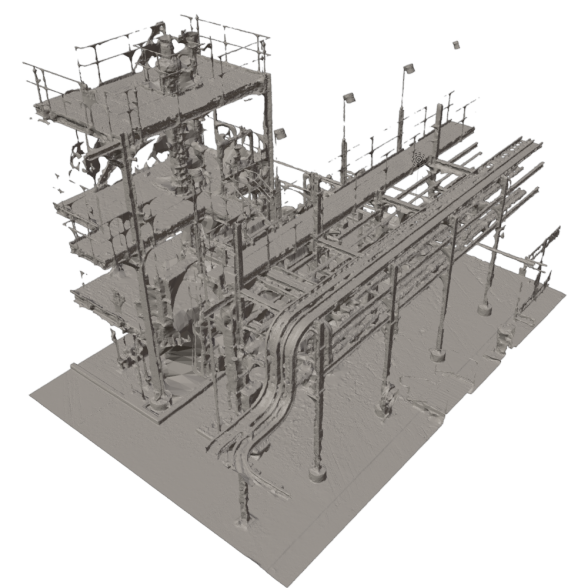
Plant refers to a glycol distillation plant at the San Jacinto College. The mesh model of the plant is obtained by processing raw scans collected from a Leica RTC360 Laser Scanner and a BLK ARC Lidar scanner. This scenario consists of 52.5M vertices and 92.0M faces, and is sized 44m $\times$ 19m $\times$ 15m.
Plant-s is a subset of the Plant scenario with size 15m $\times$ 10m $\times$ 10m, consisting of 10.4M vertices and 20.9M faces.
The results are shown below:

We investigate on the performace of IRIS-M (more efficient version of the state-of-the-art IRIS), TP (a RITA-like [1] simple inspection planner) and TP-IPIM (TP where all primitives are replaced by IPIM). From the results, we can tell IPIM save considerable memory. In the most complex scenario, IPIM enables TP to save up to $70 \times$ baseline memory (which is required regardless of what inspection algorithm is used).

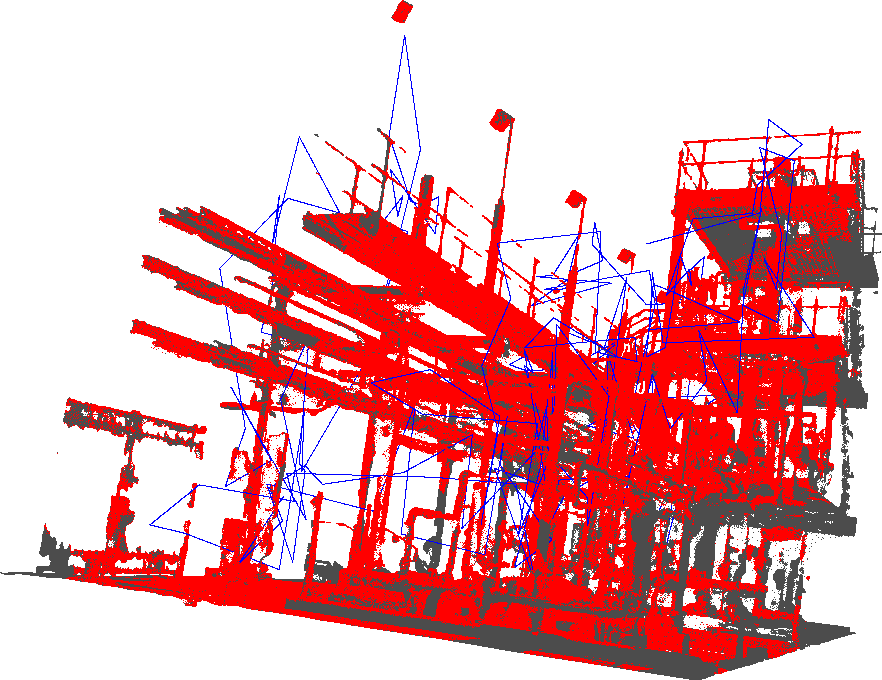
Finally, we demonstrate a sample inspection trajectory planned for three hours in the Plant-s scenario. With IPIM, even a simple inspection planner can navigate through complex and cluttered to cover more areas.

References